Блог вчителя математики Карамян М.Г.: 8 класс. Алгебра

19.05.2020
Здравствуйте, ребята!
Уважаемые восьмиклассники!
Сегодня мы пишем итоговую контрольную работу по алгебре.

Ребята, контрольные работу выполняете на двойных листах или А-4, пишите разборчиво или печатаете. Работы присылаете на мою почту, сохраняя оригинал,

до 18ч 22.05.2020

Начало первой работы:

Итоговая контрольная работа по алгебре
ученика(цы) 8-А (Б) класса ОШ №11
Ф.И.(в род. п.)
І (ІІ) вариант

І вариант

ІІ вариант

Ребята, в этой работе не выполняем задания
№6, №10 и №12;
№1 - №7(6) по1 б., №8(7) - №11(9) по2 б.

Домашнее задание.

до 18ч 22.05.2020

прислать работы на мою почту.

12.05.2020
Здравствуйте, ребята!
Уважаемые восьмиклассники!
Начиная с сегодняшнего дня выполняете две контрольные работы по вариантам.

Думаю, что не забыли свой вариант!

Ребята,контрольные работы выполняете на двойных листах или А-4, пишите разборчиво или печатаете. Работы присылаете на мою почту, сохраняя оригинал,

до 15ч 18.05.2020

Начало первой работы:

Контрольная работа по теме
"Квадратный трехчлен.Решение уравнений, приводимых к квадратным"
ученика(цы) 8-А (Б) класса ОШ №11
Ф.И.(в род. п.)

І (ІІ) вариант

Начало второй работы:

Контрольная работа по теме
"Решение уравнений.Решение задач с помощью уравнений, приводимых к квадратным"
ученика(цы) 8-А (Б) класса ОШ №11
Ф.И.(в род. п.)

І (ІІ) вариант

Вариант 3- I
Вариант 4- II

Домашнее задание.

до 15ч 18.05.2020
прислать работы на мою почту.

04.05.2020
Здравствуйте, ребята!

Уважаемые восьмиклассники! На прошлой неделе вы получили возможность пройти по два теста по алгебре и геометрии повторно, но только те, которые их не проходили! Некоторые из вас поступили некорректно, прошли тесты еще раз, а некоторые и в этот раз прошли мимо... И еще... у некоторых из вас одинаковый IP-адрес!?
А теперьВсе ваши баллы будут только вашими.
Поехали дальше! Не присылайте письменную часть Д/З, списанную откуда-то. Обращайте свое внимание на образцы оформления их. Сверьте свои записи с тем, как должно быть: Д/З на сегодня.

Переходим к изучению нового материала.

Тема. Рациональные уравнения как математические модели реальных ситуаций

Итак, мы должны научиться применять дробно-рациональные уравнения при решении задач как математического, так и прикладного содержания.
Сейчас попрошу вас быть предельно внимательными.
Умения решить подобную задачу оцениваются от 9 до 12 баллов.
Нижеследующие задачи построчно разбираете,записываете в свои тетради: №777, №782, №785, №797, №799

Обращаюсь сейчас к тем ребятам, которые хотят знать больше и иметь от 10 до 12 баллов. Предлагаю вам научиться решать более сложные уравнения, приводимые к квадратным: №766, №768

Вот теперь все!

Мы закончили курс алгебры 8 класса

Домашнее задание.
Повторить параграф 3,

пункты 18- 23 , конспект изучить;

№751(4,5),
№755(1),
№779,
№784,
№788,
№800

https://www.youtube.com/watch?v=FEF3Q_oMrh8

https://www.youtube.com/watch?v=jkRalyht1Ls

https://www.youtube.com/watch?v=PNEyytARiJg

Всем удачи! Будьте здоровы!

27.04.2020
Здравствуйте, ребята!

Учитывая ваше желание работать, я выполню перезапуск тестов по алгебре и геометрии(последние).Тесты проходят только пропустившие их, причем у вас будет только одна попытка. Поэтому, прежде чем приступать к их выполнению, изучите соответствующий теоретический материал , разберите практические упражнения:классные, и домашние.И, на будущее, заданную работу выполняйте, пожалуйста, своевременно!

Теперь обращаюсь к тем, кто хочет, может и работает на высоком уровне. Обратите внимание на нижеследующие упражнения по теме "Квадратный трехчлен" Разобрав их, советую записать решение в тетрадь.

Сейчас 13.54, это значит, кто не успел прислать д/з, проверит по моим записям. Хочу предупредить, что в новых условиях нам приходиться очень много писать , и физически нет времени переписывать. Думаю, отнесетесь к этому с пониманием. Вот задания из домашней работы.

Итак, мы научились разлагать квадратный трехчлен на линейные множители и, как вы могли заметить, тема очень важная,к ней вы будете возвращаться в следующих классах. Поэтому до 04.05.2020 вам всем нужно выполнить тест по теме "Квадратный трехчлен. Разложение квадратного трехчлена на множители".

Завдання необхідно виконати до 4 травня 11:00

Идем дальше! Сегодня научимся решать уравнения, приводимые к квадратным.

Тема. Уравнения, приводимые к квадратным.

Биквадратные уравнения

Ребята, наверняка ,исходя из приведенных примеров, вы поняли по какому алгоритму будем решать биквадраные уравнения! Да, примернно по такому.

А сейчас рассмотрим некоторые упражнения из нашего учебника.

Ребята,я рассмотрела с вами разноуровневые задания.

Внимательно, очень внимательно читаете условие (выбрав задание по своему уровню), изучаете решение, записываете в тетрадь. Всё!

Домашнее задание.

Пункт 22 , конспект изучить,
пункт 21 повторить;
№751(1,3,6),
№753(1,4),
№759(1),
№757.

https://www.youtube.com/watch?v=FEF3Q_oMrh8

https://www.youtube.com/watch?v=jkRalyht1Ls

https://www.youtube.com/watch?v=PNEyytARiJg

Всем удачи! Будьте здоровы!

Повторно!!!

Завдання необхідно виконати до 30 квітня 15:00

Завдання необхідно виконати до 30 квітня 15:00 Код доступу 283988

Итак, мы научились решать квадратные уравнения(неполные, полные), познакомились с теоремой Виета, научились применять ее. Итог вашей работы - это выполнение как домашнего задания, так и выполнение оценочных тестов.
Нелегко сегодня всем, однако каждый из нас обязан выполнять достойно свою работу.
Уважаемые восьмиклассники!
Вас убедительно просили подписывать свои работы,но никак не:

мистер Х

прорлортип

кОрОнАвИрУс

ммм

ажэажаж

Аоадартвжаиетвлпттпдвдптп

Ывапгргованпгро

Коваль Влада

Ffcg

Liza

Ыгыгыгыгы

жмых пожилой

обдолбай даждсжч...

Поскольку учеников с такими" ФИО " у нас нет, то их оценки не смогу выставить в журнал...

А сейчас переходим к изучению новой темы.

Тема. Квадратный трехчлен.
Разложение квадратного трехчлена на множители

Ответ: -1; 4

Ребята,предлагаю вашему вниманию два видеоурока.

https://www.youtube.com/watch?v=NdtSkbc_iow https://www.youtube.com/watch?v=BTjY-GRJoS8

Ребята, очень внимательно разберите нижеследующие упражнения и обязательно запишите в рабочую тетрадь.

Домашнее задание.
Пункт 21, конспект изучить;№729(3,6,8),
№731(1,3),
№733
№744(2,4,6)

Всем удачи! Будьте здоровы!

13.04.2020

Здравствуйте, ребята!

Несколько слов об оформлении письменной части домашнего задания. Ребята,изучайте образцы, которые я показываю, и по этому алгоритму выполняйте письменное решение, внимательно записывайте ответ.

Проанализируйте, сравните со своим решением, не делайте обидных ошибок!!!

Сегодня у нас заключительное занятие по теме " Квадратные уравнения. Теорема Виета"

Повторим, что нам уже известно.

Ребята! Внимательно изучите решения следующих упражнений:
№694, №697,№699, №702, №796 №710 .
Запишите в рабочую тетрадь!

№702**

Домашнее задание. Повторить пункты 18-20.

№698(1-3)№707(1,2), №711(по желанию).

Обязательно пройти тесты на оценку:

1. Код доступу 329822

join.naurok.ua (Теорема Виета)

Завдання необхідно виконати до 21 квітня 11:00

2.Код доступу 570031

join.naurok.ua (Контрольная работа" Квадратные уравнения. Теорема Виета" )
Завдання необхідно виконати до 21 квітня 11:00

https://www.youtube.com/watch?v=YctnR1JX1WM

https://www.youtube.com/watch?v=71hK9V0AtYg

https://www.youtube.com/watch?v=ES3_OF6hHP8

https://www.youtube.com/watch?v=vKliFIbK-VY

Всем удачи! Будьте здоровы!!!

До встречи 21.04.2020

Здравствуйте, ребята!
Мы изучаем тему " Неполные квадратные уравнения" .
Конспект по теме у вас есть, а решение письменной части жду до 20.03.20.
1. https://www.youtube.com/watch?v=NWivkaBqui0
2.https://www.youtube.com/watch?v=V1VAjc9OjXM
3.https://www.youtube.com/watch?v=nouhGuAmB3

Здравствуйте, ребята! Сегодня 20.03.2020.
Хочу напомнить, что письменная часть до 12б. выполняется полностью.
Пояснения по №623:

Убедительно прошу вас работать по этому алгоритму!

Уважаемые 8- классники!!! Сейчас 20.41 22.03.2020. Письменную часть д/з вы уже должны были прислать до 20.03!!! К тому же решение № 623 уже на странице!

30.03.2020

Тема. Формула корней квадратного уравнения

I.

Квадратное уравнение

— это уравнение вида
a x² + b x + c = 0,

где х-переменная, а, b ,c - некоторые числа, причем, где a не равно 0.

Геометрический смысл

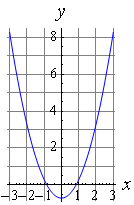
Графиком квадратичной функции является парабола. Корнями квадратного уравнения называют абсциссы точек пересечения параболы с осью абсцисс. Если парабола, описываемая квадратичной функцией, не пересекается с осью абсцисс, уравнение не имеет действительных корней. Если парабола касается оси абсцисс в одной точке (вершине параболы), уравнение имеет один действительный корень (также говорят, что уравнение имеет два совпадающих корня). Если парабола пересекает ось абсцисс в двух точках, уравнение имеет два действительных корня.

Если коэффициент a положительный, ветви параболы направлены вверх, если отрицательный — ветви параболы направлены вниз. Если коэффициент b положительный, то вершина параболы лежит в левой полуплоскости, если отрицательный — в правой полуплоскости.

$Парабола$

Вывод формулы для решения квадратного уравнения
Формулу для решения квадратного уравнения
a x² + b x + c = 0 можно получить так:

перенесем c в правую часть a x² + b x = - c

умножим уравнение на 4a (2a x)² + 4a b x = - 4a c

добавим b² к обоим частям (2a x)² + 4a b x + b² = b² - 4a c

в левой части выделим полный квадрат (2a x + b)² = b² - 4a c

извлечем квадратный корень 2a x + b = ± √b² - 4a c

перенесем b в правую часть 2a x = - b ± √b² - 4a c

разделим уравнение на 2a

x = -b ± √b² - 4a c

2 a

Дискриминант квадратного уравнения

Дискриминантом

квадратного уравнения называют число равное
D = b² − 4ac

Квадратное уравнение с действительными коэффициентами может иметь от 0 до 2 действительных корней в зависимости от значения дискриминанта:

при D > 0 корней два, и они вычисляются по формуле

x_1,2 = -b ± √D

2 a
при D = 0 корень один (два равных или совпадающих корня), кратности 2:

x = -b

2 a
при D < 0 действительных корней нет.

Теорема Виета

Приведенным квадратным уравнением

называется уравнение, в котором коэффициент при x² равен единице. Такое уравнение может быть получено делением всего выражения на коэффициент a:
x² + px + q = 0, где p = ba, q = ca

Теорема Виета

Сумма корней приведённого квадратного уравнения

x² + px + q = 0 равна коэффициенту p, взятому с обратным знаком, а произведение корней равно свободному члену q:
x₁ + x₂ = -p,

x₁x₂ = q.

Разложение квадратного уравнения на множители

Если известны оба корня квадратного уравнения, его можно разложить по формуле

ax² + bx + c = a(x - x₁)(x - x₂)

II.

Примеры решения квадратных уравнений

Например.
Найти корни квадратного уравнения: 2x² + 5x + 3 = 0
D = 5² - 4·3·2 = 25 - 24 = 1; 1>0.

x₁ =	-5 + √1	= -1,
	2·2

x₂ =	-5 - √1	= -1	1
	2·2		2

Ответ: -1;-1,5

Упражнение. Решите квадратное уравнение:

-3x² + 18 x + 81 = 0

Квадратное уравнение

x₁ =

x₂ =

Домашнее задание. П. 19 изучить, №633(2,4), №635(2,4,6.8,10,12), №639(1).
Тест Код доступу 934563 join.naurok.ua

06.04.2020

Здравствуйте, ребята!

Прежде,чем начать изучение нового материала, хочу напомнить:

теоретическую часть переписывать в тетрадь нет необходимости(у вас есть учебник);
если кто-то хочет сохранить конспект себе на будущее, то,пожалуйста;
подписывайте свои работы;