8 класс. Геометрия

13.05.2020

Здравствуйте, ребята!

Уважаемые восьмиклассники, мы завершили изучение программного материала по геометрии за курс 8 класса. Поэтому сегодня мы пишем контрольную работу по повторению и обобщению учебного материала.

Эту работу вы пишите на двойных листах, затем присылаете мне на почту до 12ч 20.05.2020.

Начало работы.

                    Итоговая контрольная работа

                    по геометрии за курс 8 класса

                             ученика(цы) 8-А класса ОШ №11

                                    Ф.И. (в род. п.)

        

                                      I(II) вариант

Домашнее задание.

Выполнить  контрольные работы.
№1 - №6 по 1 б., №7 - №9 по 2 б.( с полным обоснованием) .
Работы присылаете на мою почту
 до 12ч  20.05.2020

Удачи всем! Будьте здоровы!

06.05.2020
Здравствуйте, ребята!
   Сегодня мы завершаем работу по многоугольникам и их площадям. 

Прочитайте условие каждой из следующих задач по учебнику,попробуйте на черновике решить,затем сравнить, проверить и только потом записать решение в тетрадь по образцу.

Ребята, аналогично и вы оформляете решения задач из домашнего задания.

 

 Домашнее задание.

Повторить пункты 19 - 23;
  
№690, №710, №715, №746, №783

https://www.youtube.com/watch?v=lcEQemXqbf8

https://www.youtube.com/watch?v=5pc5lMVwzoM

https://www.youtube.com/watch?v=-Xuc7DpePC8

Код доступу 278780

 join.naurok.ua

                                                Завдання необхідно виконати до  12 травня 14:00

Всем удачи! Будьте здоровы!

28.04.2020
Здравствуйте, ребята!
   Сегодня мы продолжим работу по многоугольникам и их площадям, выведем формулы для вычисления площади параллелограмма, треугольника и трапеции. Но все по порядку.
   Сначала проверьте правильность решения и оформления решения задач из домашнего задания.

У кого совпало - молодцы!!!





А теперь поехали дальше!
Сначала посмотрите эти видеоуроки.

https://www.youtube.com/watch?v=lcEQemXqbf8

https://www.youtube.com/watch?v=5pc5lMVwzoM

https://www.youtube.com/watch?v=-Xuc7DpePC8

Тема. Площадь параллелограмма,
            треугольника и трапеции
          

Площадь параллелограмма

Необходимо определить, что такое высота параллелограмма.

Это перпендикуляр, проведённый из любой точки стороны параллелограмма к прямой, содержащей противоположную параллельную сторону. Обычно высоту проводят из вершины параллелограмма. Так как параллелограмм имеет две пары параллельных сторон, то он имеет высоты двух различных длин.

Высота BE, проведённая между длинными сторонами, короче высоты BF, проведённой между короткими сторонами.

Так как стороны ромба одинаковы, то высоты ромба также одинаковы: BE=BF.

 

Площадь произвольного параллелограмма

Площадь параллелограмма равна произведению высоты и стороны, к которой проведена высота.

Проведём высоты из двух вершин B и C к стороне AD .

Прямоугольные треугольники ABE и DCF равны (равные гипотенузы как противоположные стороны параллелограмма и равные катеты как расстояние между параллельными прямыми).

Параллелограмм ABCD и прямоугольник EBCF — равновеликие, так как состоят из равных фигур:

SABCD=SABE+SEBCD;SEBCF=SEBCD+SDCF.

Значит, площадь параллелограмма определяется так же, как площадь прямоугольника:

SEBCF=BE⋅BC;SABCD=BE⋅BC=BE⋅AD.

Если обозначить сторону через a, высоту — через h, то:

Sп−гр.=   


   a⋅h.

Для определения площади параллелограмма можно использовать короткую сторону и высоту, проведённую к короткой стороне.

Площадь ромба

Диагонали ромба в точке пересечения делятся пополам, они перпендикулярны и делят ромб на четыре равных прямоугольных треугольника.

SABCD=4⋅SABO=4⋅BO⋅AO2=2⋅BO⋅AO.

Формула определения площади ромба:

Sромба=d1⋅d22.

Эта формула справедлива для определения площади любого четырёхугольника, если его диагонали перпендикулярны.

Так как диагонали квадрата равны, то для определения площади квадрата в формуле достаточно длины одной диагонали:

Sквадрата=d22.

Площадь произвольного треугольника

Так как диагональ параллелограмма делит его на два равных треугольника, то площадь треугольника равна половине площади параллелограмма.

 

Sтреуг=aha2, где h — высота (на рисунке — BE), проведённая к стороне a (на рисунке — AD).

Для определения площади треугольника можно использовать любую сторону и высоту, проведённую к этой стороне.

Удобно иногда использовать формулу Герона, если известны длины всех трёх сторон треугольника.

SΔ=p(p−a)(p−b)(p−c)−−−−−−−−−−−−−−−−−√;p=a+b+c2

— формула Герона, где a, b и c — стороны треугольника, p — полупериметр треугольника.

Площадь прямоугольного треугольника

Так как катеты прямоугольного треугольника взаимно перпендикулярны, то один катет может быть высотой, а другой катет — стороной, к которой проведена высота. Получаем формулу:

S=a⋅b2, где a и b — катеты.

Для прямоугольного треугольника также можно применять формулы площади произвольного треугольника.

Пример:

1. Вычислим площадь треугольника со сторонами 17 см, 39 см, 44 см.

Решение:

p=17+39+442=50;SΔ=50⋅(50−17)⋅(50−39)⋅(50−44)−−−−−−−−−−−−−−−−−−−−−−−−−√=50⋅33⋅11⋅6−−−−−−−−−−√==25⋅2⋅3⋅11⋅11⋅2⋅3−−−−−−−−−−−−−−−−−√=5⋅2⋅3⋅11=330(см2).

Чтобы легче было вычислить корень, необходимо не перемножать все числа, а раскладывать их на множители: a⋅a−−−−√=a.

Формулу Герона можно использовать для вычисления высоты треугольника.

Пример:

2. Вычислим меньшую высоту треугольника, стороны которого равны 15 см, 13 см, 4 см.

Решение:

используем две формулы вычисления площади:  SΔ=aha2 и SΔ=p(p−a)(p−b)(p−c)−−−−−−−−−−−−−−−−−√.

Меньшая высота в треугольнике — та, которая проведена к большей стороне, поэтому a= 15 см.

SΔ=p(p−a)(p−b)(p−c)−−−−−−−−−−−−−−−−−√=16⋅1⋅3⋅12−−−−−−−−−√=24(см2).

Составляем уравнение:

                        

15⋅h2=24∣∣⋅215⋅h=48;h=4815=3,2(см).

Иногда формула Герона используется для вычисления площади параллелограмма, если даны стороны параллелограмма и его диагональ.

Пример:

3. Дан параллелограмм со сторонами 17 см и 39 см, длина диагонали равна 44 см. Вычислим площадь параллелограмма.  

Решение:

диагональ делит параллелограмм на два равных треугольника. Используем результат, полученный в первом примере:

Sпараллелограмма=2⋅SΔ=2⋅330=660(см2).

Площадь трапеции

Трапеция имеет одну пару параллельных сторон, следовательно, имеет одну высоту — перпендикуляр, проведённый между параллельными сторонами.

Чаще всего высоту трапеции проводят из вершин или через точку пересечения диагоналей.

Площадь трапеции определим как сумму площадей треугольников, на которые трапецию делит диагональ.

 S

ABCD=SABD+SDBC;SABCD=AD⋅BE2+BC⋅DF2=AD⋅BE2+BC⋅BE2==(AD+BC)⋅BE2.

Если обозначить параллельные стороны (основания) трапеции через a и b, высоту через h, то:

Sтрап=a+b2⋅h.

Обрати внимание!

Важные следствия:

1. Если высоты треугольников равны, то их площади относятся как длины оснований.

2. Если основания треугольников равны, то их площади относятся как длины высот.

3. Если высоты треугольников равны и их основания равны, то они равновелики, например, медиана делит треугольник на две равновеликие части.

Запомните эти формулы!!!

Попробуем применить изученные формулы площадей параллелограмма, треугольника и трапеции при решении задач.

Ребята,решения этих задач, разобрав, обязательно записываете в тетрадь.





На сегодня  все!








Домашнее задание.  
Изучить пункты 21 - 23;
 повторить пункты 19;20,
№701, №724, №732, №773

https://www.youtube.com/watch?v=lcEQemXqbf8

https://www.youtube.com/watch?v=5pc5lMVwzoM

https://www.youtube.com/watch?v=-Xuc7DpePC8

Всем удачи! Будьте здоровы!

Ждите тесты (оценочные)!









22.04.2020
Здравствуйте, ребята!

   Сегодня мы переходим к изучению последней темы курса геометрии 8 класса
              "Многоугольники. Площадь многоугольника"
   Изучив теоретический материал по этой теме, вы сможете ответить на вопрос о многоугольнике, его элементах и свойствах;узнаете, что такое площадь многоугольника, по каким формулам вычисляются площади прямоугольника и квадрата, параллелограмма,треугольника и трапеции. А самое главное, научитесь решать задачи на нахождение площадей этих многоугольников.  

                                                                       Поехали!


Тема. Многоугольники и их свойства.                         Площадь многоугольника.
           Площадь прямоугольника

Многоугольник — это простая замкнутая ломаная линия и конечная часть

плоскости, которую она ограничивает.

Вершины ломаной линии называются вершинами многоугольника, а её звенья — сторонами многоугольника.

Отрезок, соединяющий две вершины, не лежащие на одной стороне, называется диагональю многоугольника.

  

A, B, C, D, E — вершины;
AB, BC, CD, DE, AE — стороны;
AC, AD, BE, BD, CE — диагонали.

Многоугольник, у которого все углы меньше 180°, называется выпуклым многоугольником.

Пятиугольник ABCDE является выпуклым многоугольником. 

Сумма углов выпуклого n-угольника

В общем случае многоугольник можно назвать n-угольником, это означает, что у данного многоугольника n сторон и n вершин.

Сумма углов выпуклого n-угольника равна 180°⋅(n−2).

Любой выпуклый многоугольник можно разделить на треугольники. Количество треугольников на 2 меньше, чем количество сторон в многоугольнике.

Сумма внутренних углов любого треугольника равна 180°.

Поэтому сумма углов выпуклого n-угольника равна 180°⋅(n−2).

Пример:
1. Вычисли сумму внутренних углов выпуклого одиннадцатиугольника.

Можно нарисовать рисунок, но это не обязательно для решения задачи.
Используем формулу:
180°⋅(n−2)=180°⋅(11−2)=180°⋅9=1620°.

Ответ: 1620*

2. Определи, сколько углов у многоугольника.

Ответ:  угл(-ов, -а).

  

Название данного многоугольника:

• восьмиугольник
• шестиугольник
• пятиугольник
• девятиугольник
• треугольник
• семиугольник
• четырёхугольник
• десятиугольник

3.Вычисли сумму внутренних углов восьмиугольника.

Выбери правильную формулу:

• 180°⋅(n−3)
• 180°⋅n
• 360°⋅(n−2)
• 180°⋅(n−2)

Ответ: сумма внутренних углов восьмиугольника равна °.

            Основные факты о площади 

Можно сказать, что площадь многоугольника — это величина, обозначающая часть плоскости, которую занимает данный многоугольник.
 За единицу измерения площади принимают площадь квадрата со стороной 1 см, 1 мм и т.д. (единичный квадрат). Тогда площадь будет измеряться в см2, мм2 соответственно.
 Иными словами, можно сказать, что площадь фигуры — это величина, численное значение которой показывает, сколько раз единичный квадрат умещается в данной фигуре.


                Свойства площади 

1.    Площадь любого многоугольника — величина                         положительная. 
2.    Равные многоугольники имеют равные площади. 
3.    Если многоугольник составлен из нескольких                          многоугольников, то его площадь равна
        сумме площадей этих многоугольников. 
4.    Площадь квадрата со стороной a равна a2.
        (а в квадрате!)



                   Площадь прямоугольника


Теорема:  Площадь прямоугольника со сторонами a и b                           равна   S=ab.

Ребята, а теперь обратите внимание на решения задач и их оформление. Советую записать  в тетрадь.

На сегодня все


                               Домашнее задание.
                                  Пункты 19;20

https://www.youtube.com/watch?v=6SN38rZpaxs&list=PLBnDGoKqP7bY_V8lEYj_3d3AenlZrYfgW&index=3&t=0s

https://ppt-online.org/537449

№648(2), №650,
№653, № 655,№673.

                                                                                                            

15.04.2020

Здравствуйте, ребята!
Сегодня мы завершаем изучение темы
   "Решение  прямоугольных треугольников".
Вам предстоит выполнить два итоговых теста на оценку. Но сначала я покажу, как нужно было решить из домашнего задания задачи и письменно оформить их.
 Поехали!!!

Ребята, эти задачи не из легких, а достаточного и высокого уровней. Поэтому, как следует разберите эти задачи  и запишите решение в тетрадь!
Прежде, чем вы начнете проходить тестирование, повторите теоретический материал! Подписывайтесь под своими Ф.И.



Домашнее задание.            Повторить: параграф 3(пункты 15-18), материалы                                                                         предыдущего занятия.

https://www.youtube.com/watch?v=f_klVl93C08

https://naurok.com.ua/prezentaciya-perpendikulyar-i-pohila-144390.html

https://vseosvita.ua/library/urok-doslidzenna-z-geometrii-perpendikular-i-pohila-137290.html

http://www.myshared.ru/slide/1002538/

Тесты по теме "Решение прямоугольных треугольников"
Тест 1.   Код доступу 437771

             join.naurok.ua

Завдання необхідно виконати до  22 квітня 11:00

Тест 2. Код доступу 197111

           join.naurok.ua

                 https://naurok.com.ua/test/join?gamecode=197111

Завдання необхідно виконати до  22 квітня 11:00

Всем удачи! Будьте здоровы!!!















07.04.2020

Здравствуйте, ребята!
Сегодня мы повторим знакомую нам тему и продолжим развивать наши практические навыки. Поехали!!!



Тема урока.   Перпендикуляр и наклонная.   Решение                                     прямоугольных треугольников

Чтобы вы повторили первую тему, пересмотрите нижеследующие материалы.

https://www.youtube.com/watch?v=f_klVl93C08

https://naurok.com.ua/prezentaciya-perpendikulyar-i-pohila-144390.html

https://vseosvita.ua/library/urok-doslidzenna-z-geometrii-perpendikular-i-pohila-137290.html

http://www.myshared.ru/slide/1002538/

       Не для кого не секрет что вся элементарная геометрия пришла к нам в основном с Египта и Греции. В далекие и древние времена геометрия использовалась как наука для измерения земли, а также очень тесно при строительстве.     Все теоремы, законыи аксиомы выводили и доказывали,   чтобы облегчить измерительные или строительные работы.             Сегодняшняя тема была очень важна для людей того времени так как перпендикуляр и наклонная основные ориентиры при работе такого типа.

         Существует много гипотез относительно техники строительства египетских пирамид. Очевидным является то, что техника эта менялась со временем, т.е. более поздние пирамиды строились иначе, нежели более ранние.

Техника строительства Великих пирамид по Геродоту

        Нашим единственным письменным источником, в котором описывается процесс строительства пирамид, служит II книга «Истории» Геродота, посетившего Египет ок. 450 г. до н. э. Не говоря на языке египтян, Геродот должен был делать записи со слов греческих поселенцев, проживавших в стране, а также — через переводчиков — со слов представителей египетского жречества. О том, как строили Великие пирамиды две тысячи лет назад до него, ему определённо было трудно узнать, поскольку это вряд ли было известно и самим египтянам.

  Одни были обязаны перетаскивать к Нилу огромные глыбы камней из каменоломен в Аравийских горах (через реку камни перевозили на кораблях), а другим было приказано тащить их дальше до так называемых Ливийских гор. Сто тысяч людей выполняло эту работу непрерывно, сменяясь каждые три месяца. Десять лет пришлось измученному народу строить дорогу, по которой тащили эти каменные глыбы, — работа, по-моему, едва ли не столь же огромная, как и постройка самой пирамиды. Сооружение же самой пирамиды продолжалось двадцать лет.

                                                                                            

                          Перпендикуляр и наклонная

И так начнем с простейшего и давайте повторим что такоее перпендикуляр и наклонная.

                            Перпендикулярные прямые

                                            

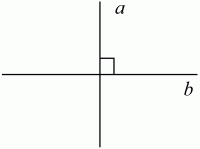
   Определение. 
Две прямые называются перпендикулярными, если они пересекаются под прямым углом.

Перпендикулярность прямых обозначается знаком ⊥ Запись а ⊥ b читается: Прямая а перпендикулярна прямой b.

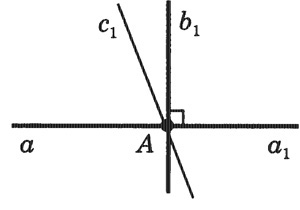
Теорема. 
Через каждую точку прямой можно провести перпендикулярную ей прямую, и только одну.

         

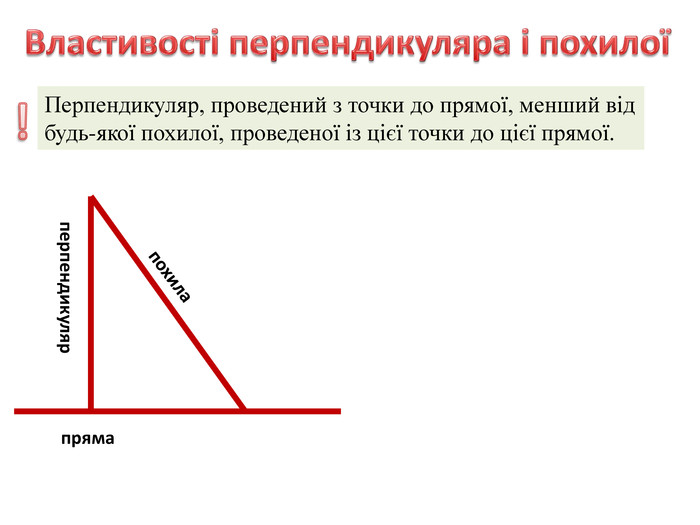
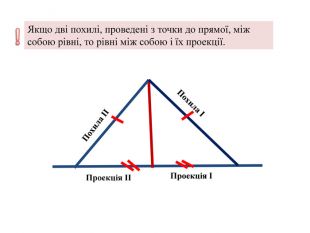
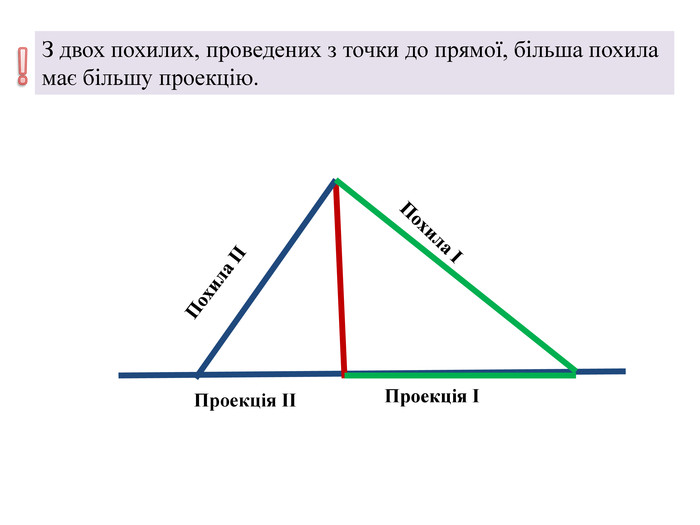
Задача №1

В равнобедренном треугольнике ABC с основанием AC, равным 37, внешний угол при вершине B равен 60^o. Найдите расстояние от вершины C до прямой AB.

                                                           
                                                                       № 635

Домашнее задание.            Повторить пункты 15-18, №628, №633, №636,

 https://www.youtube.com/watch?v=f_klVl93C08

https://naurok.com.ua/prezentaciya-perpendikulyar-i-pohila-144390.html

https://vseosvita.ua/library/urok-doslidzenna-z-geometrii-perpendikular-i-pohila-137290.html

http://www.myshared.ru/slide/1002538/

Тест по теме "Решение прямоугольных треугольников"

Код доступу 664739

                          join.naurok.ua

Здравствуйте, ребята!

Тема урока.     Решение прямоугольных треугольников

          

Ребята, решения задач жду до 24.03.20.

1.https://www.youtube.com/watch?v=FHazsBry3To

2.https://www.youtube.com/watch?v=Hz1Xt8TtlSg&t=29s

25.03.2020                             Решения задач из д/з.

                                                        

 01.04.2020

Тема урока.     Решение прямоугольных треугольников

• 
  

• Ребята,посмотрите эту презентацию http://www.myshared.ru/slide/1004455/ , выполняйте предложенные задания сначала самостоятельно, затем проверьте себя.
• Теперь задачи №615, №619, №621, №623, №629, изучите, решения запишите в тетрадь.

• Домашнее задание. Повторить пункты 15-18, №616, №620, №622, №624,№631(доп.)

                                     Тест   Код доступу 723589

                                       join.naurok.ua

                                            (до 08.04,   11ч )